Simulating randomness
mar benavides nebot
ies gelida – gelida
What is randomness? Most of us have made this question ourselves sometimes. For me, it was broad and mysterious field. I had no information about it and lack of knowledge made me feel curious about the insights of randomness.
I started the project with one word, randomness, from where I had to initiate my research. After acquiring some knowledge about the subject, I decided to focus on random numbers, the methods to generate them and their applicability in our lives.
The work begins with an introduction to two subjects, that are essential to understand how random numbers can be generated: modular arithmetic and probability theory. Modular arithmetic is a system of arithmetic for integers, where numbers “wrap around” upon reaching a certain value: the modulus. Probability theory is the branch of mathematics concerned with probability and the analysis of random phenomena.
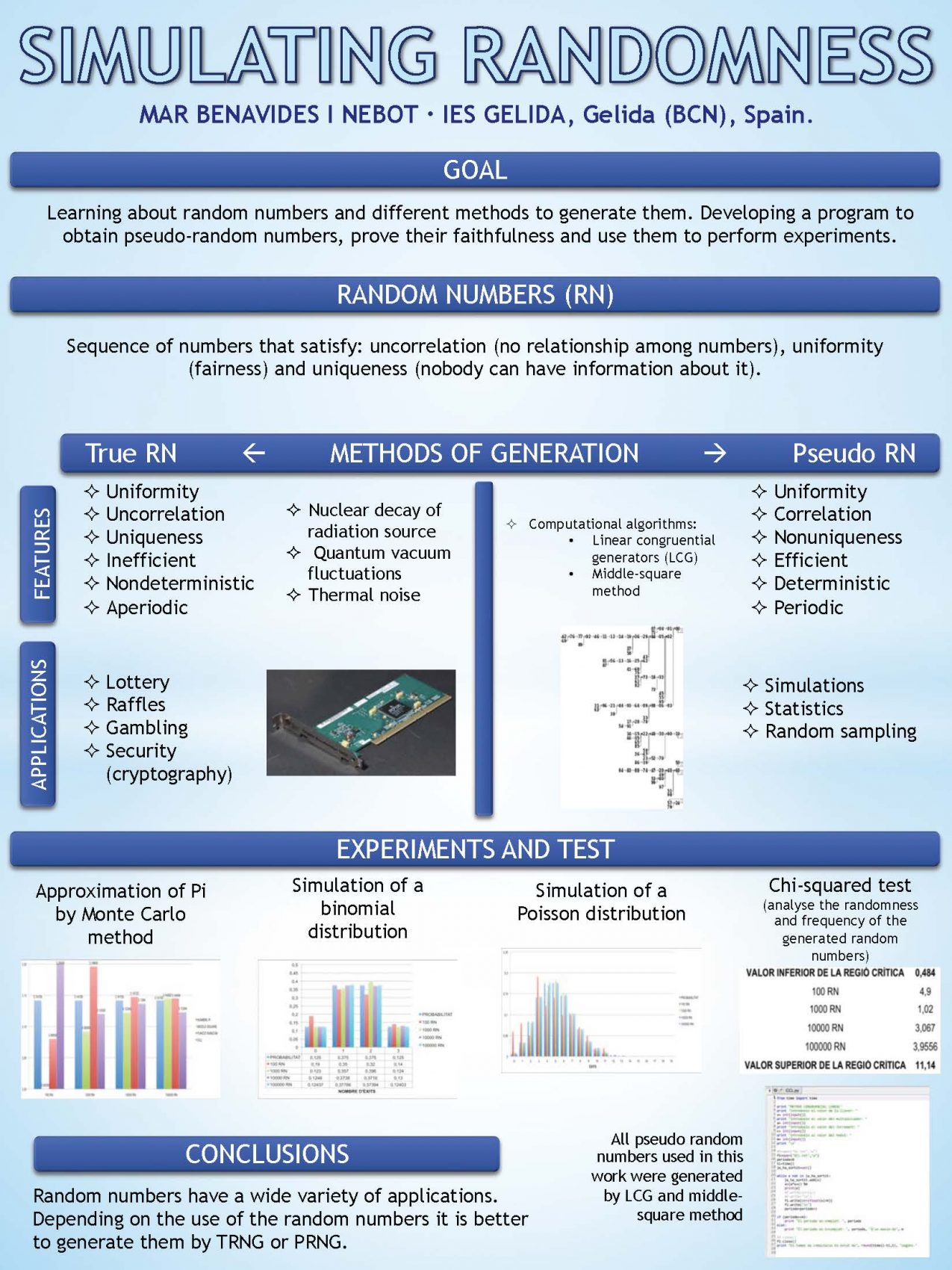
After that, it follows with a study of random numbers, i.e., sequences of numbers with three properties: uncorrelation, uniformity, and uniqueness. There are two principal methods to generate them depending on their application:
- True random numbers generators. They use physical and quantum physical features like thermal noise, quantum vacuum fluctuations and nuclear decay of radiation source, which assures uncorrelation, uniformity and uniqueness. They can be used in lottery, raffles, gambling and security (cryptography). It is the most secure system that guarantees nobody can obtain information about the sequences.
- Pseudo-random number generators. They are algorithms that generate uncorrelated sequences of numbers starting from a known seed value. There are often used to perform simulations and generate random samples. These algorithms the simplest and most efficient method to generate random numbers.
Since it was not in my hands to create a true random number generator, I decided to write two computer algorithms in Python: the linear congruential generator and middle-square method. The longest sequence had 1,000,000 random numbers, which I used to perform some experiments: obtaining an approximation for Pi using the Monte Carlo method and simulating binomial and Poisson probability distributions and analysing them with the chi-squared test.
As a conclusion, the choice of the best method to generate random numbers mostly depends on the application domain where then have to used